Two Orders From Chaos

November 26, 2019

A summary of this paper which provides a coherent framework for analysing hysteresis and phase coexistence in bistable systems. All errors and omissions are mine entirely. All good stuff is down to the authors.

Sometimes, it is remarkable how simple the world really is. In my small room there are trillions upon trillions of particles, billions of which are jiggling and flying across the room randomly. Despite this frenetic atomic bombardment, objects are distinct. Even though each molecule moves almost independently, I can easily perceive the water in my glass. Somehow, there is order among this apparent chaos. And this order is especially obvious in systems which we call bistable.

You create a bistable system every time you make a cup of tea. As you boil the kettle, the temperature of the water within rises. Every second, the water molecules jiggle more and more, until they can no longer contain themselves. At a critical temperature — the boiling point — the inexorable logic of thermodynamics kicks in, and the water molecules jump into the air, freed from hydrogen bonds by excess heat. If steam didn’t leak, your kettle would have two stable solutions: either full of liquid, or full of vapour.

Bistable systems are extremely general. We encounter them all the time. When we turn the taps on at the sink, there is a critical point after which water begins to flow. Bistability occurs in global systems as well, including Earth’s magnetic field (it reverses every 20,000 years or so) and climate (both warm periods and Ice Ages are stable states). Each system I mentioned has different microscopic properties, but amazingly, their global behaviour can be captured by the same mathematical models of bistability.

Many bistable systems have a property called phase coexistence. This means that for some special conditions, the two stable states can occur at the same time. When you boil the kettle, the water doesn’t stay entirely liquid, then flash into the gaseous state all at once. Instead, as you near the boiling point, some excited water molecules fly off, escaping their slower counterparts. Likewise, if you turn the tap at a critical angle, water occasionally drips out of the faucet.

Stable states and phase coexistence can be captured by the free energy of a dynamical system. If the system has no noise, it will occupy the state with the lowest free energy — the most stable state. This corresponds to the minimum of the free energy profile below. F is the free energy, while X is some general order parameter.

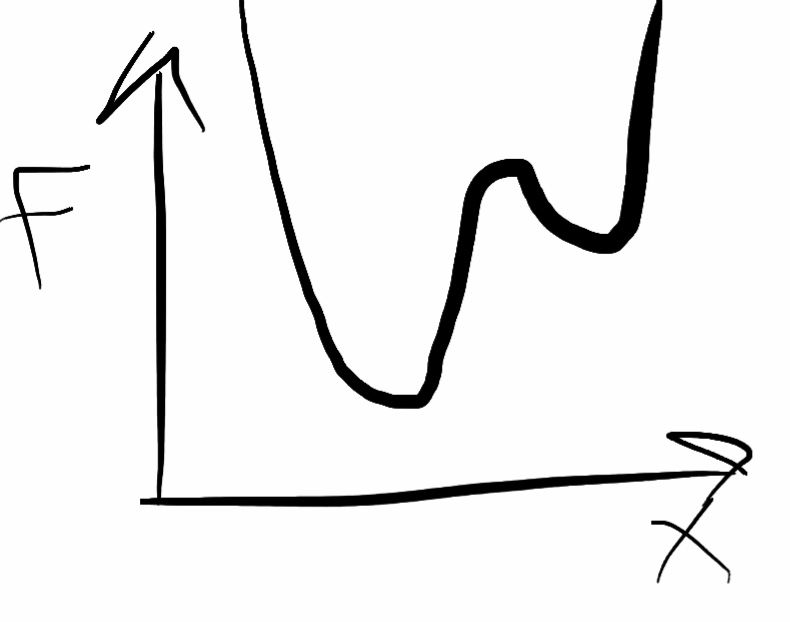
Phase coexistence occurs when two or more minima are at equal height, like below. In this case, both states will be occupied.

Another property of bistable systems is hysteresis. Hysteresis is the dependence of the state of a system on its history. It is a delay between cause and effect. The thermostat in your house exhibits hysteresis. It doesn’t try to maintain a specific temperature — otherwise it would have to be switched on forever. Instead it has a specified temperature range. When the preset temperature is reached it switches off. It only switches on again when the range is exceeded. Hysteresis is the delay between the change in temperature, and the response of the thermostat.

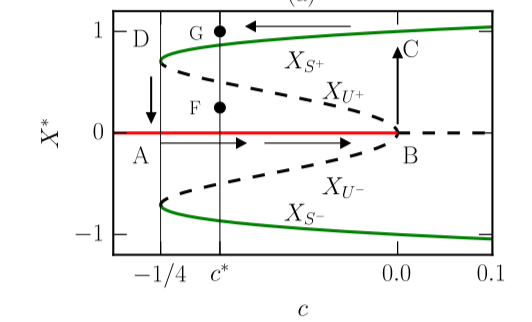
The model provided in this paper explains zero-noise hysteresis in bistable systems. Hysteresis is often displayed in a loop, which can be seen below. For a state starting at A, as c is varied, there is no change in X⁺, until at state B, X⁺ jumps from 0 to 1, following the green curve. If c is then decreased, X⁺ follows the green curve left, before jumping from state D back to state A.

Bistable systems get even more interesting when noise is added. Due to thermal fluctuations — the minuscule molecular movement mentioned earlier — real systems are noisy. Adding noise to a bistable system gives it random bursts of energy, like a physical system might get from the environment. This allows the system to jump from one stable state to another, extending the range of phase coexistence.

The most interesting feature of the model is the effect of noise on hysteresis. A small amount of random noise in a bistable system reduces the hysteresis, because the noise provides the energy to kick the system earlier from one steady to state to the next. In the diagram below, the hysteresis loop without noise is ABCD, while with noise it is reduced to HEFG.

Hysteresis is a source of uncertainty in many mechanical and electrical measuring devices (including thermostats). Suggesting ways to limit this uncertainty is highly valuable. Noise in biological processes is vital in keeping systems in out-of-equilibrium stability and driving them between steady states. This paper provides some mathematical justification for this empirical fact.

From magnets to kettles and many things in between, bistable systems show the similarity between a variety of fields; finding simple order amongst the seeming chaos.